Mise en oeuvre d'un correcteur P.I.D. avec un système du troisième ordre

Comprendre l'électronique par la simulation.
par Serge Dusausay  Espace lecteur  plan du site

Article 28	Quelques informations supplémentaires des pages 169 à 176 du livre.
Pour cet article, consultez également le courrier des lecteurs

Ce complément d'article traite la mise en oeuvre d'un correcteur PID.
Le système à asservir est du 3 ème ordre. Il modélise le processus équipé de son capteur de chaîne de retour.
L'entrée est une tension, la sortie est une tension.

On se propose de ne présenter ici que les grandes lignes principales :

1) de tester le processus seul et de comparer avec la simulation,
2) de simuler le circuit dans un asservissement avec un correcteur K_p réglé à la valeur dite de "juste oscillation",
3) d'en déterminer les coefficients du PID (méthode de Ziegler et Nichols),
4) de simuler le système corrigé,
5) de rechercher une amélioration de la réponse, à l'aide de la simulation.
6) Essai pratique.

1) Réponse indicielle du processus.
Le graphe ci dessous montre les courbes expérimentales:
- trace supérieure : signal d'entrée : échelon d'amplitude 2 V
- trace inférieure : signal de sortie.


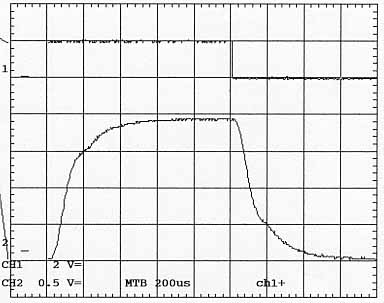Réponse à l'échelon du système du 3 ème ordre seul, réel
200 us / carreau	haut : CH1 : 2 V / c	bas : CH2 : 0,5 V / c

Interprétation :
Le temps de réponse à 5 % est environ 350 us.
L'amplification statique est voisine de 1.
Remarque : en fait, ce système du troisième ordre est la mise en cascade du premier ordre de l'article 06 et du deuxième ordre de l'article 07.

Le graphe ci dessous montre le résultat de la simulation:
- trace supérieure : signal d'entrée : échelon d'amplitude 2 V
- trace inférieure : signal de sortie.

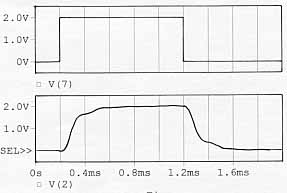Réponse à l'échelon du système du 3 ème ordre seul, simulé

Interprétation :
Le temps de réponse à 5 % est de 335 us.
L'amplification statique est de 1.

Remarque : il est bien évident que ces valeurs étaient connues avant de lancer la simulation, car elles sont indirectement dans le fichier d'entrée.

On peut donc considérer que le processus simulé est très voisin du processus réel, dans ces conditions d'observations.
La dispersion observée peut avoir des conséquences dans un système bouclé.

2) Réponse indicielle du système bouclé, juste oscillant.
On insère le processus dans un asservissement avec un correcteur proportionnel uniquement, K_p.
La réponse "juste oscillante" est d'avoir des conditions d'instabilité telles que le système bouclé oscille en régime quasi sinusoïdal.
Cette expérience est parfois impossible physiquement, pour des raisons de sécurité, domaine de fonctionnement...
Aussi il est judicieux de faire appel à la simulation pour déterminer la valeur de K_p qui rende instable (oscillations entretenues) le système bouclé.

Plusieurs essais ont été effectués : la valeur limite de K_p correspondant à l'oscillation est délicate à trouver en simulation : cela dépend du temps d'observation (donc du temps de simulation) pour apprécier le régime quasi sinusoïdal.
Le graphe ci dessous montre pour K_p = 3,2 :
- signal d'entrée : on conserve l'échelon d'amplitude 2 V
- signal de sortie

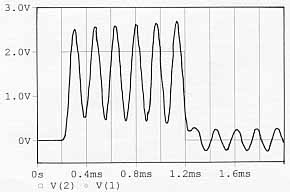Réponse temporelle simulée, système juste oscillant

Interprétation :
Avec cette valeur de K_p, nous avons réalisé ici un oscillateur, qui répond également au signal d'entrée.
Pour cet essai, le signal d'entrée est un terme supplémentaire.
On peut lire :
T_osc = 166 us
On adopte :
K_posc = 3.2

Remarques :
- Dans ce type d'oscillateur en régime quasi sinusoïdal, l'amplitude est directement liée au conditions initiales lors du départ de l' oscillation. C'est ce qu'on observe très nettement ici.
- pour K_p > 3.6 environ, la sinusoïde est d'amplitude divergente.

3) Détermination des coefficients du P.I.D.
On utilise la méthode de Ziegler et Nichols.
K_p = 0,6 K_posc, soit 1.92
T_i = 0.5 T_osc, soit 83 us
T_d = 0.12 T_osc, soit 20 us

4) Réponse indicielle du système bouclé, avec PID réglé.
Continuons d'exploiter la simulation pour observer le comportement de l'asservissement dans ces conditions.
Le graphe ci dessous montre le résultat de la simulation:
- trace supérieure : signal d'entrée : échelon d'amplitude 2 V
- trace inférieure : signal de sortie.

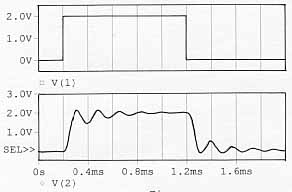Réponse temporelle simulée, processus dans un asservissement avec PID déterminé par Ziegler et Nichols.

Interprétation :
Le système est stable.
L'erreur de position est nulle.
Le temps de réponse à 5 % est de 550 us.
Remarque : Si on est moins exigeant pour apprécier la valeur finale, par exemple à +- 6 %, le temps de stabilisation n'est plus que 400 us.

5) Amélioration du PID.
Toujours par l'apport de la simulation, on peut rechercher un autre triplet de valeurs qui permette une meilleure réponse indicielle.

Le graphe ci dessous montre le résultat de la simulation :
avec K_p = 1.7 ; T_i = 40 us ; T_d = 30 us .
- trace supérieure : signal d'entrée : échelon d'amplitude 2 V
- trace inférieure : signal de sortie.

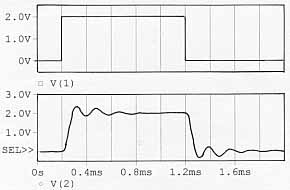Réponse temporelle simulée, processus dans un asservissement avec PID optimisé.

Interprétation :
Le système est stable.
L'erreur de position est nulle.
Le temps de réponse à 5 % est de 320 us.
La réponse présente 2 dépassements marqués, de 17 % et 12,5 %.

Remarque :
Comme indiqué en page 175 du livre, la dispersion des valeurs des paramètres est un argument important à prendre en compte lors de la réalisation concrète du correcteur. Dans ces simulations, on peut remarquer qu'il faut une dynamique de réglage d'environ :
+- 10 % sur K_p
+- 50 % sur T_i
+- 50 % sur T_d
et ce pour chercher un optimum.

6) Essai pratique
L'essai sur table a été réalisé :
- on positionne les valeurs de K_p, T_i, T_d proche des résultats de simulation, on connecte, et ... le système est stable.
- on recherche une amélioration de la réponse indicielle.

Le processus du troisième ordre présenté ci dessus, inséré dans un système bouclé à retour unitaire, avec :
K_p = 2.2,
T_i = 37 us,
T_d = 50 us,
donne :


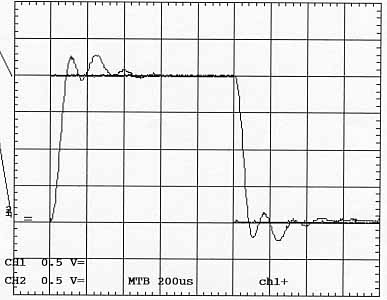Réponse à l'échelon du système bouclé avec PID optimisé
200 us / carreau	CH1 : 0,5 V / c	CH2 : 0,5 V / c

On peut mesurer :
- pas d'erreur statique,
- un temps de réponse tr5% = 300 us,
- deux dépassements marqués d'environ 13 %.

Nous sommes à des résultats similaires de la simulation.

Il est possible d'avoir d'autres résultats, comme un temps de réponse de 200 us environ, mais un premier dépassement de 37 %.

En conclusion, l'apport de la simulation Pspice a permis de prédéterminer un correcteur PID de façon sûre et fiable.
Les écarts, dûs à une modélisation insuffisament précise, sont néanmoins acceptables pour dimensionner un correcteur PID.

fin de l'article 28

lire le courrier des lecteurs sur cet article

retour à l'écran d'accueil

Comprendre l'électronique par la simulation. par Serge Dusausay Espace lecteur plan du site