Comprendre l'électronique par la simulation.
par Serge Dusausay            Espace lecteur
                    Courrier


 Article 28
 courrier du
 13 09 2003
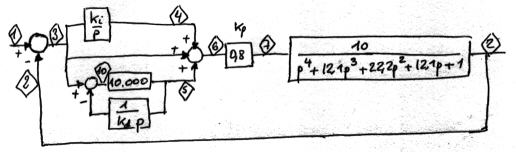
  Question :    Votre article sur le PID (28) est clair, mais le fichier syspid.cir ne l'est pas beaucoup...
Vous ne montrez pas les correspondances entre les numéros de noeuds et le contenu du correcteur PID, et je ne comprends pas grand chose dans la constitution du correcteur en lui même.
Pouvez-vous me donner un peu plus de renseignements ? (un petit schéma S.V.P. ?)

 Réponse :  

Bonjour,

j'avoue que, contrairement aux autres articles, il manque en effet une description fidèle du schéma simulé, notamment dans la constitution du correcteur P.I.D. Cela est dû à ce que le fichier utilise des sources commandées, ce qui nous éloigne d'un montage électronique "réel". D'ailleurs, tout le montage exploite ce genre de sources, ce qui présente l'avantage d'être simulable avec la version d'évaluation du CD ROM.
Aussi, j'ai préféré ne donner que l'essentiel pour la compréhension de l'article (ce qui me semble réussi, d'après votre première remarque) en ne spécifiant que les principaux numéros de noeuds : entrée de consigne, signal d'erreur, et signal de sortie, et en faisant abstraction de l'intérieur du correcteur.
Votre question montre que vous désirez "rentrer" dans le fichier syspid.cir, et là, c'est moins évident que dans les autres fichiers.cir du livre.
Alors, comme un schéma vaut mieux qu'un grand discours, et que c'est ce que vous attendez, voici le complément d'information tant attendu...

quelques explications supplémentaires
comment lire le fichier syspid.cir

Le correcteur suit exactement la structure C(p) donnée en page 170 du livre.
Ici, il est câblé entre V(7) et V(3).

Il a été utilisé un procédé, (indiqué en bas de page 176), pour réaliser le dérivateur :
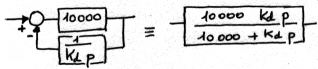un dérivateur à base d'un intégrateur
comment faire un dérivateur à base d'un intégrateur


En effet, si vous tracez la réponse harmonique de ce montage :
FTBF
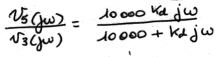la transmittance résultante du dérivateur équivalent

vous remarquerez que dans une gamme de pulsation telle que Kdw << 10000, ce montage est équivalent à jKdw, qui est donc un dérivateur.

Dans l'article 28, l'application numérique est Kdmax = 5.
L'inégalité devient 5 w << 10000, soit f << 318 Hz.
C'est cohérent avec l'arrêt des runs de simulations (Diagramme de Black donné en page 173) à 100 Hz.

Rappelons que ce procédé de fabriquer un dérivateur à base d'intégrateur est pour éviter des problèmes de convergence, typique à Pspice, problèmes qu'on ne trouve pas sur un simulateur comme Matlab Simulink par exemple.

Il est évident, qu'en pratique, on peut réaliser un dérivateur à base d'amplificateur opérationnel, comme celui proposé dans l'article 25. Dans ce cas, il faut tenir compte qu'il est également inverseur, et que, comme tous montages à base d'amplificateurs opérationnels, est limité en fréquence. Ce dernier point n'est pas critique pour la gamme utilisée dans notre article.

retour à l'écran d'accueil, début du site