Comprendre l'électronique par la simulation.
par Serge Dusausay  Espace lecteur  plan du site


 Article 27 
   Quelques informations supplémentaires des pages 163 à 168 du livre.
réponsePour cet article, consultez également le courrier des lecteurs


L'intégrateur à capacités commutées simulé dans l'article a été réalisé sur une carte de travaux pratiques. Nous montrons ci-dessous la très forte similitude entre les résultats de simulation du livre, et les résultats expérimentaux.


Rappel : errata en pages 166 et 167 (3.c et 3.d) :
il faut lire intégrateur inverseur (et non intégrateur).
C'est clairement indiqué en page 164, mais ce n'est pas répété par la suite.


La carte expérimentale délivre :

- une horloge double, fréquence 50 kHz, temps de non-recouvrement = 1,25 us
- les interrupteurs commandés réalisés par des DG211/212
- une source sinusoïdale d'impédance interne 100 Ohm, de fréquence 1 kHz, et d'amplitude proche de 4 V
- une cellule à base d'amplificateur opérationnel TL081
- C = 2,2 nF; C' = 33 nF
- une résistance supplémentaire de 100 kOhm mise en parallèle avec C' afin de pallier le défaut de l'amplificateur opérationnel (IBIAS), comme indiqué page 294, notion de cours n°1. Cette résistance a une valeur suffisamment élevée pour négliger son rôle dans l'intégrateur.


D'après le paragraphe 3.c de la page 166,
la résistance équivalente vaut 9,1 kOhm
la constante de temps vaut alors 0,3 ms.

Selon une application numérique identique à la page 167,
à la fréquence 1 kHz, le module de la fonction de transfert vaut 0,53.

2 signaux sont présentés ci dessous :

- le signal sinusoïdal d'entrée,
- la sortie de l'intégrateur inverseur.

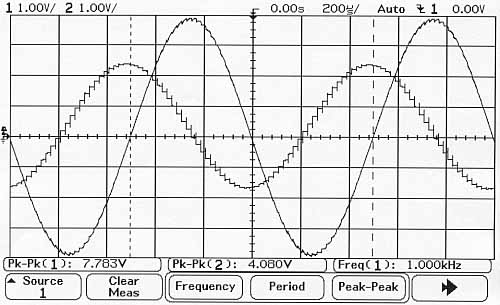recopie d'écran scannérisée
Fonctionnement de l'intégrateur inverseur à capacités commutées
200 us / carreau Voie 1 : 1 V / c Voie 2 : 1 V / c

Interprétation :

1) vue macroscopique
Il s'agit d'une vue d'ensemble.

- l'entrée est sinusoïdale, la sortie est cosinusoïdale : ceci est cohérent avec la fonction d'intégrateur inverseur
- le signal d'entrée présente 7,8 V peak to peak (sinusoïde de 3,9 V d'amplitude), celui de sortie, à cette fréquence, environ 4,1 V peak to peak, soit un coefficient d'amplification de 0,52, valeur prédéterminée précédemment.

2) vue microscopique
Il s'agit d'une vue détaillée.

L'équation aux différences (page 165) donne :
SnT-S(n-1)T= -C/C' e(n-1)T
appliquée aux valeurs numériques de notre circuit :
SnT-S(n-1)T= -0,67 e(n-1)T
Par exemple, au maximum de e(n-1)T, soit 3,9 V :
La "marche d'escalier" a une amplitude de 0,67 x 3,9 soit 0,26 V.
C'est la valeur mesurée en exploitant un zoom à l'oscilloscope, valeur que l'on peut néanmoins voir à cette échelle.


3) Quelques remarques :

- La source sinusoïdale dispose d'une résistance interne. (Il s'agit d'une protection en cas de fausse manipulation en Travaux Pratiques).
La conséquence est de provoquer une chute de tension à chaque appel de courant, lors de la fermeture de l'interrupteur int1. Ce courant est d'autant plus intense que la tension d'entrée est élevée, le condensateur C étant déchargé entièrement à chaque fermeture de int1.
On voit nettement un défaut aux extremum de la sinusoïde.

- La sortie de l'intégrateur montre un décalage de tension. Ce phénomène est traditionnel avec ce genre de montage. Réduire la résistance de 100 kOhm diminuerait cet offset, mais finirait par réduire le gain statique.

- Le signal de sortie est très bruité : des brefs pics de tension apparaissent à chaque commutation. Par un emploi judicieux de l'oscilloscope, on peut masquer une partie de ce défaut à l'affichage, mais ce n'est qu'une apparence.

Il est évident qu'une simulation simple ne montre pas tous les défauts rencontrés dans la pratique...Mais les analyses présentées dans l'ouvrage sont parfaitement en accord avec la pratique.

Industriellement, on réalise les capacités commutées en circuits intégrés, et non en composants discrets. Par rapport à des résistances discrètes, les avantages sont les suivants :
- gain de surface (donc de coût) surtout pour des résistances de forte valeur, malgré le circuit d'horloge nécessaire,
- stabilité en température,
- bien qu'il soit difficile de fabriquer un condensateur précis à mieux de 10% (imprécision dans la géométrie de gravure), il est possible de fabriquer des rapports de condensateurs précis à 1% près. On exploite le fait que les erreurs géométriques se compensent. Or les fonctions de transfert des circuits exploitent les rapports de capacités.
- on peut réaliser une résistance variable par action sur l'horloge.

En contrepartie, la présence des transitions d'horloge augmentent le bruit, ce qui exclut les capacités commutées à certains domaines de l'électronique.
à titre d'information, voici ci dessous la carte de travaux pratiques sur laquelle a été réalisée la manipulation :
carte de T.P.
Carte de Travaux Pratiques "capacités commutées"

C'est une carte développée en interne, qui dispose :

d'une partie commande qui génère les signaux (visible en bas sur la photo) :
- logiques (à base de circuit programmable), comme Phi1, Phi2
- analogique, comme les tensions sinusoïdales.

et d'une partie opérative, sur laquelle on trouve :
- des douilles accèdant aux interrupteurs DG211/212, aux A. Op,
- des cavaliers portant les condensateurs (en blanc sur la photo)
.
Cette carte permet par simple modification de fils et/ou d'emplacement des cavaliers, de changer le montage.
C'est ainsi qu'elle est exploitée aussi pour l'article 36.

fin de l'article 27

lire le courrier des lecteurs sur cet article

retour à l'écran d'accueil