calculer et réaliser un petit oscillateur simple à transistor

Comprendre l'électronique par la simulation.
par Serge Dusausay  Espace lecteur  plan du site

Article 23	Quelques informations supplémentaires des pages 139 à 144 du livre.
Pour cet article, consultez également le courrier des lecteurs

Cet article montre la théorie et les simulations d'un oscillateur.
Ce complément montre ce qu'on obtient en faisant l'essai "sur table" de cet oscillateur.

Est donné également par la suite un complément de théorie -bien utile pour certains- sur l'étude harmonique du circuit déphaseur.

Le montage a été câblé selon le schéma de la page 140 du livre. Notons que les transistors étaient des NPN 2N1893

Le signal de sortie est :


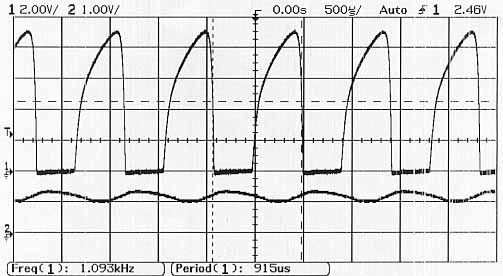Le montage oscille à 1 kHz
20 us / carreau	haut : Voie 1 : 2 V / c	bas : Voie 2 : 1 V / c

Interprétation :
- C'est équivalent à ce qui est montré dans le livre :
trace supérieure : V(1)
trace inférieure : V(5)
- Par honnêteté scientifique, indiquons que les conditions de polarisation n'étaient pas identiques à celles données en page 140 ou 141.
En effet, comme rappelé en page 144, (pour aller plus loin), un changement de transistor (ou une dispersion de ses caractéristiques) peut amener à des courants de polarisation différents, et par suite, à une répartition de potentiel différente. Ce phénomène est dû au choix de l'étage de polarisation, qui ne présente pas une robustesse vis à vis de ce phénomène. La conséquence est un coefficient d'amplification différent de celui prédéterminé.
Mais dans notre cas, l'amplification apportée par l'association Q1 Q2 demeure supérieure à celle nécessaire pour être en régime quasi-sinusoïdal, et l'oscillation a lieu.

Le montage oscille à la fréquence 1,093 kHz.

- Le transistor Q2 travaille en bloqué / saturé, comme expliqué en page 143

- On montre également le signal de retour, après le condensateur de liaison.
On retrouve essentiellement le terme fondamental (le signal V(1) qui a traversé un filtre passe bas d'ordre 3), et des harmoniques.
Ce signal de retour est en opposition de phase par rapport à V(1), (si tant est que l'on peut parler de déphasage sur des signaux non sinusoïdaux).
La partie alternative (0,41 V peak to peak) est portée par une composante continue de 1,2 V, qui a pour origine les 2 tensions VBE.

Dernière remarque :
Il est prudent de choisir un point de masse judicieux qui permet d'éviter des bruits HF lors de la mesure à l'oscilloscope. Un classique condensateur de découplage sur le + 15 V est conseillé.

Annexe : Etude détaillée du circuit déphaseur

Le triple circuit RC rencontré dans ce montage est parfois une source d'erreurs pour les étudiants, en ce qui concerne le calcul de la fonction de transfert et de sa réponse harmonique.

Alors, puisqu'il m'est donné la possibilité d'intervenir dans le bon sens ...

1) La fonction de transfert N'EST PAS : 1/(1+jRCw)³

Cela sous-entendrait que les 3 cellules RC ne se perturbent pas entre elles...
Dans notre schéma page 141, (le classique réseau avec 3 résistances identiques et 3 condensateurs identiques), il est absolument faux de raisonner avec 3 cellules identiques du premier ordre cascadées indépendantes.

Remarque, pour mettre les points sur les i et les barres sur les t : cela serait éventuellement possible dans 2 cas :

-cas n°1 : un montage suiveur intercalé entre la sortie de la cellule i et l'entrée de la cellule i+1, donc 2 montages suiveur au total. Ces amplis d'isolement assureraient, sur chaque cellule, une impédance d'entrée infinie, et une impédance de sortie nulle.

-cas n°2 : des valeurs numériques aux composants choisies pertinement, comme par exemple:
la première cellule présente R = 10 Ohm et C = 8,2 uF,
la deuxième R = 1 kOhm et C = 82 nF,
la troisième R = 100 kOhm et C = 820 pF.
Ces valeurs numériques présentent le même produit RC à chaque étage (82 us), et des impédances telles qu'un étage i+1 ne perturbe quasiment pas l'étage i. Dans ces conditions, la mise en cascade peut se faire sans se préoccuper des impédances de charge.
Mais ce réseau complet présente, à 1 kHz par exemple, une impédance d'entrée d'environ 21,8 Ohm et de sortie environ 218 kOhm, ce qui peut être une contrainte lors de sa mise en oeuvre dans son environnement.

2) Comment calculer la fonction de transfert :

On peut établir les équations de mailles et de noeuds, ou réduire le schéma d'étage en étage en appliquant le théorème de Thevenin. Ces procédés de calcul, faisables aisément pour une double cellule (comme par exemple l'article 8 page 60), deviennent fastidieux pour une triple cellule.

Il est plus rationnel de faire appel au calcul matriciel, en exploitant la matrice de chaîne, notée K.
Parmi les nombreuses représentations de quadripole sous forme matricielle, la matrice de chaîne, est définie par :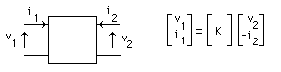

Les paramètres de cette matrice sont :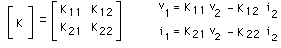
paramètres de la matrice K

Par exemple, une simple impédance série peut être décrite par :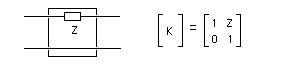
matrice K d'une impédance série

Ou, autre exemple, une impédance parallèle par :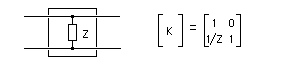
matrice K d'une impédance parallèle

La mise en cascade de 2 quadripôles est équivalente à un quadripôle.
La matrice K de ce quadripole équivalent est le produit des matrices K des 2 quadripôles.
C'est la principale propriété de la matrice de chaîne: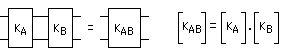
cascade de quadripôle

Exploitons cette propriété pour construire la matrice K du circuit RC :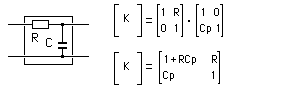

De même, le triple circuit RC :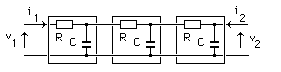

admet donc une matrice de chaine équivalente :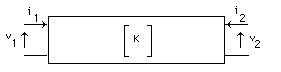
est équivalent à

qui est, d'après ce qui vient d'être écrit :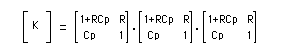
soit

On remarque que, à courant de sortie nul, la fonction de transfert (sous forme de Laplace) du réseau est l'inverse du coefficient K₁₁.
Dans le but de déterminer cette fonction de transfert, il n'est donc pas utile de calculer les 4 coefficients de la matrice K, mais seulement K₁₁.
Ce qui aboutit à :
K₁₁ = R³C³p³ + 5 R²C²p² + 6 RCp + 1

La réponse en excitation sinusoïdale est obtenue en remplacant p par jw, ce qui est la relation L(jw) donnée en bas de la page 140 du livre.

3) Comment tracer la réponse harmonique :

La réponse de L(jw) peut se représenter par les diagrammes de Bode :
on détermine les expressions de module et phase et on trace point par point, la variable étant la fréquence ou la pulsation.
Dans notre application, le plus important est le passage à - 180°, et de connaître la fréquence et l'atténuation correspondantes.
Mais si l'on désire faire un tracé sur tout l'axe des fréquences, on peut s'aider par le tracé de branches asymptotiques intermédiaires.
En effet, nous allons montrer que L(jw) peut être remplacée par une mise en facteur de 3 fonctions du premier ordre.
Par simplicité d'écriture, reprenons le calcul par les transformées de Laplace.

On cherche à résoudre :
R³C³p³ + 5 R²C²p² + 6 RCp + 1 = (1+t₁p)(1+t₂p)(1+t₃p)
En développant, on identifie terme à terme :
t₁t₂t₃ = R³C³
t₁t₂ + t₁t₃ + t₂t₃ = 5 R²C²
t₁ + t₂ + t₃ = 6 RC

Système qui aboutit à :
t₁ = 0,308 RC
t₂ = 0,643 RC
t₃ = 5,048 RC

Il est donc possible de tracer la réponse harmonique de L(jw) à l'aide des tracés asymptotiques de 1/(1+jwt₁), 1/(1+jwt₂), 1/(1+jwt₃) et ce, en module et phase.

L'application numérique donne 3 pulsations de cassure :
1/t₁ = 8424 rad/s
1/t₂ = 4035 rad/s
1/t₃ = 514 rad/s
soit des fréquences de cassure de 1340 Hz, 642 Hz et 82 Hz respectivement.
La réponse harmonique est donc (tracée ici "à la main"):

Remarques :

- Sur la courbe de 20 log {module}, il a été placé 2 axes horizontaux : pulsation et pulsation réduite.

- Sur la courbe de phase, il a été placé l'axe des fréquences, en regard direct des pulsations de la courbe du module.

- Le tracé des courbes réelles est grandement aidé par celui des asymptotes intermédiaires.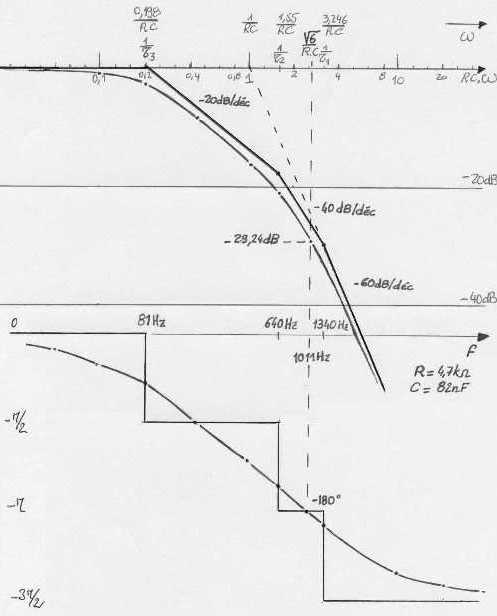

réponse harmonique

Interprétation :

- Le circuit déphaseur présente un plateau 0 dB en très basse fréquence : l'analyse du schéma (où le montage est alors équivalent à 3 R sans courant les traversant), ainsi que l'examen de la fonction de transfert (L(jw) tend vers 1 quand w tend vers 0) le confirment.

- En très haute fréquence, on trouve une pente asymptotique du troisième ordre, ce qui cohérent avec le schéma. D'ailleurs avec w tendant vers l'infini, L(jw) est équivalent à 1/(RCjw)³. Cette expression montre que l'extrapolation de l'asymptote à - 60 dB/décade passe par 1/(2 pi RC).

- Le calcul (page 141) montre que la phase passe par - 180 ° à la pulsation 2,45/RC.
A cette pulsation le réseau atténue d'un coeffecient de 29, soit une chute de gain de 29,24 dB. On retrouve ces valeurs sur le tracé.

Bien entendu, il est plus rapide de tracer L(jw) par un moyen plus moderne, comme la simulation Pspice. En page 142 du livre, est présentée la réponse harmonique (module et phase) de l'association ampli + réseau déphaseur.

fin de l'article 23

lire le courrier des lecteurs sur cet article

retour à l'écran d'accueil

Comprendre l'électronique par la simulation. par Serge Dusausay Espace lecteur plan du site