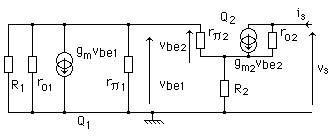
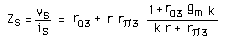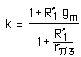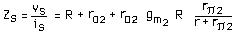Comprendre l'électronique par la simulation.
par Serge Dusausay  Espace lecteur  plan du site


 Article 21 
   Quelques informations supplémentaires des pages 127 à 134 du livre.


En page 129, il est montré un avantage de la source de Wilson : sa grande impédance de sortie. La simulation a donné 2,3 MOhm (bas de page 129), et ce, avec des transistors "dégradés".
On se propose ici de retrouver cette valeur par le calcul. Il s'agit donc d'un complément au paragraphe 1.

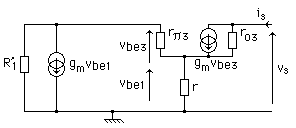
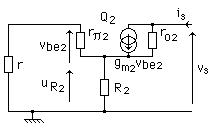
De plus, en page 130, on montre la conséquence d'insérer une résistance d'émetteur. Est proposé ci-dessous, en complément du paragraphe 2, le calcul de l'impédance de sortie de la source de courant.

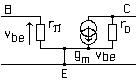
Remarque : pour des raisons d'affichage avec Netscape, il est écrit PI au lieu du symbole grec pi.


COMPLEMENT AU PARAGRAPHE 1

On se propose de calculer l'impédance de la source de Wilson, dont le schéma est donnné en 1.b.
Il nous faut le schéma petits signaux du montage complet.
La source V1 est constante, et donc ne présente aucune variation en dynamique. Dans le schéma dynamique, elle apparait donc en court-circuit.
Chaque transistor est modélisé par le quadripôle linéaire rPI, gm vbe, r0 comme montré ci dessous :
modèle petits signaux du transistor
modèle petits signaux du transistor

Le schéma du montage devient, en petits signaux :
schéma petits signaux
schéma petits signaux de la source de Wilson de la page 128

Nous avons la présence de :
résistance équivalente

d'où, en posant R'1 = R1 // r01
et r = rPI1 // rPI2 // r02 // 1/gm
et en remarquant que vbe1 = vbe2
et que, par IC1 = IC2 = IC3, on a : gm1 = gm2 = gm3 = gm
on dispose du schéma simplifié suivant :

schéma petits signaux simplifié
schéma petits signaux réduit

Calculons l'impédance de sortie vs / is

1) Donnons les équations qui régissent le circuit :

- la tension de sortie est :
vs = ur03 + vbe1   (1)

- la tension collecteur émetteur de Q3 est :
ur03 = r03 (is - gm vbe3)   (2)

- le noeud de courant en émetteur de Q3 donne :
is = (vbe1 / r) - (vbe3 / rPI3)   (3)

- la tension aux bornes de R'1 s'écrit :
vbe1 + vbe3 = - R'1(vbe3 / rPI3 + gmvbe1)    (4)

2) Réduisons ce jeu d'équations :

d'après (3) : vbe3 = rPI3( vbe1 / r   -   is )

d'après (4) : vbe3 = - vbe1 ( 1+R'1gm) / (1+R'1/rPI3)   (4')

Par simplicité d'écriture, posons :
expression de k

Eliminons vbe3 de ces deux dernières expressions :
rPI3 ( vbe1 / r   -   is ) = - k vbe1
Il vient :
vbe1 = is (r rPI3) / (k r + rPI3)    (34)

avec (1) et (2) formons :
vs = r03 is - r03 gm vbe3 + vbe1

ce qui, d'après (4'),
vs = r03 is + r03 gm k vbe1 + vbe1 = r03 is + vbe1( 1+ r03 gm k )

et, en exploitant (34), on aboutit à :

relation de l'impédance de sortie
impédance de sortie de la source de Wilson


3) Application numérique :
D'après les informations données en page 128, 129 :
r01 = r02 = r03 = 50 kOhm
IC = 1 mA, d'où gm = 0,04, et par suite 1/gm= 25 Ohm
ß = 100, d'où IB = 10uA, d'où rPI3 = 2,5 kOhm

Par conséquence :
R'1 = 13,45 k // 50 k = 10,6 kOhm
r = 2,5 k // 2,5 k // 50 k // 25 = 25 Ohm
k = 81,1

et Zs = 2,29 MOhm,
ce qui est la valeur indiquée par Pspice (page 129).

4) Remarque intéressante : on peut déterminer une valeur approchée à Zs :
On remarque que r01 >> R1 d'où R'1 = R1
ainsi que 1/gm << rPI1 // rPI2 // r02 d'où r = 1/gm

par IC1 = IC2 = IC3, et même tension d’Early, on a : r01 = r02 = r03 que l’on pose à r0
Or, par r0= VA / IC = VA / (gm VT), il vient : r0 gm = VA/VT>>1

Simplifions l'expression de expression de k

numérateur : Par rPI = ß /gm, il vient : 1+ R'1 gm = 1 + R1 gm = R1 gm
dénominateur : de même il vient : 1 + R'1/ rPI3 = 1 + R1 / rPI3 = 1 + R1gm/ß = R1gm/ß

soit : k = ß

Nous avons également r0 gm k >> 1
L’expression de Zs devient, après des simplifications évidentes : ß r0/2
Par rapport au miroir simple, l’apport de Q3 a multiplié d’un coefficient ß/2 la résistance de sortie.
L'application numérique de ce calcul approché aboutit à 100 50k / 2, soit 2,5 MOhm, ce qui est l'ordre de grandeur.

COMPLEMENT AU PARAGRAPHE 2

On montre en page 130 une évolution du schéma du miroir de courant (figure du paragraphe 1.a.) pour former une source de courant constant (figure du paragraphe 2.a.).
Il est intéressant de calculer également son impédance de sortie.
En effet, sa forte valeur est aussi une propriété intéressante de ce circuit.

Le calcul qui suit est similaire au précédent :

- schéma petits signaux du montage complet,
- source E1 en court-circuit dans le schéma dynamique,
- transistor modélisé par rPI, gm vbe, r0.


schéma petits signaux
schéma petits signaux de la source de courant page 130

En posant :
r = R1 // r01 // 1/gm1 // rPI1

on dispose du schéma simplifié suivant :

schéma petits signaux simplifié
schéma petits signaux réduit

Calculons l'impédance de sortie vs / is

tension de sortie :   vs = ur02 + uR2    (1)
tension vce de Q2 :   ur02 = r02 (is - gm2 vbe2)   (2)

Posons R = R2 // (r + rPI2)
tension aux bornes de R2 :   uR2 = is R    (3)
pont diviseur :   vbe2 = - uR2 (rPI2/r+rPI2)    (4)

Par (3) et (4) :   vbe2 = - R is (rPI2/r+rPI2)   (34)
mis dans (2) :   ur02 = r02 is + r02 gm2 R is (rPI2/r+rPI2)   (234)
(234) et (3) dans (1) :   vs = is (r02 + r02 gm2 R (rPI2/r+rPI2)) + R is
aboutit à :
relation de l'impédance de sortie
impédance de sortie

Application numérique :
Dans ce circuit les transistors sont donnés à ß = 250 et VAF = 130 V (lire le fichier source.cir rappelé en page 134)
Nous pouvons déduire, en première approximation :
r01 = 130/1m = 130 kOhm
r02 = 130/34u = 3,8 MOhm
IB1 = 1 m / 250 , d'où rPI1 = VT/IB1 = 6500 Ohm
IB2 = 34 u / 250 , d'où rPI2 = VT/IB2 = 191 kOhm
gm1 = IC1 / VT = 1 m / 26 m = 0,04 A/V d'où 1/gm1 = 25 Ohm
gm2 = IC2 / VT = 34 u / 26 m = 1,3 mA/V d'où 1/gm2 = 764 Ohm
R1 = 29 kOhm (R4 dans le schéma de l'application)
R2 = 2,7 kOhm (R3 dans le schéma de l'application)

Il vient :
r = 29 k // 130 k // 6,5 k // 25 = 25 Ohm
R = 2,7 k // (25 + 191 k) = 2,7 kOhm
D'où, derniers calculs faits :
Zs = 17,14 MOhm

Remarques intéressantes :
1) Si on fait tendre R2 vers 0, on retrouve Zs = r02 ce qu'un simple examen du schéma montre.
2) vu les applications numériques, on peut faire les approximations suivantes :
r = 1/gm1 (= 25 Ohm)
R = R2 (= 2,7 kOhm)
rPI2 >> r
r02 >> R
et par simple conséquence : Zs = r02 (1 + R2 gm2)
Soit ici, 3,8 MOhm (1+3,51) = 17,14 MOhm
ce qui montre le rôle de R2 dans l'impédance de sortie.


fin de l'article 21

retour à l'écran d'accueil