Comprendre l'électronique par la simulation. par Serge Dusausay Espace lecteur plan du site
Article 19 |
Quelques informations supplémentaires des pages 115 à 120 du livre. |
|
L'échantillonnage est une fonction de l'électronique fondamentale dès lors que l'on
étudie le traitement du signal. Le livre présente la théorie et la simulation. Or, le montage échantillonneur ainsi que le filtre de reconstitution simulés dans l'article ont été réalisés sur une carte de travaux pratiques. Nous montrons ci-dessous que les relévés expérimentaux sont en parfait accord avec les résultats présentés dans l'ouvrage. De plus, nous traitons par la suite le cas de l'échantillonneur bloqueur |
 | |||
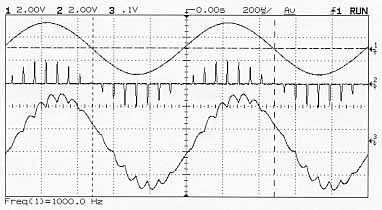
| Sinusoïde, échantillonnage, et reconstitution sommaire | |||
| 200 us / carreau | Voie 1 : 2 V / c | Voie 2 : 2 V / c | Voie 3 : 0,1 V / c |
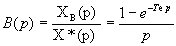
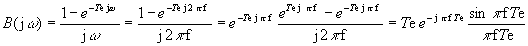
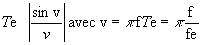
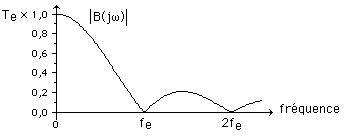
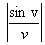 sont exactement à fe, 2fe, 3fe...
sont exactement à fe, 2fe, 3fe...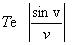 par la fonction bloqueur.
par la fonction bloqueur. 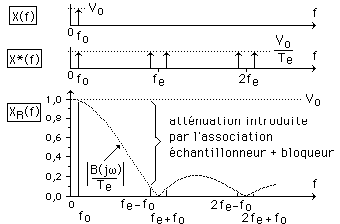
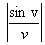 . Il ne subsiste alors que le spectre de x(t).
Dans ces conditions, le bloqueur fait office de filtre passe-bas.
Un filtre supplémentaire coupant après fmax peut être utilisé,
mais son rôle est moins critique.
. Il ne subsiste alors que le spectre de x(t).
Dans ces conditions, le bloqueur fait office de filtre passe-bas.
Un filtre supplémentaire coupant après fmax peut être utilisé,
mais son rôle est moins critique.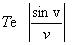
| 1 kHz | 15 kHz | 17 kHz | |
| v =PI (f/fe) | 0.196 | 2.945 | 3.338 |
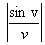
|
0.993 | 0.066 | 0.058 |
| 1.987 V | 0.1325 V | 0.117 V |
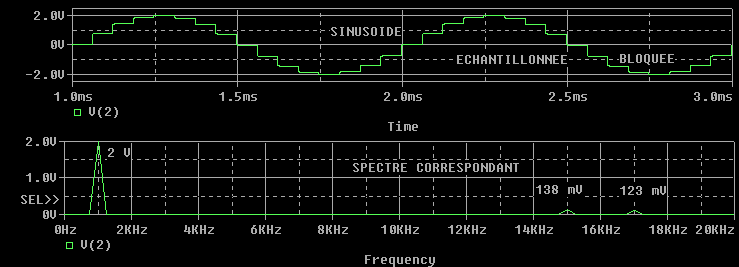 |
| Après une simulation transitoire, et FFT correspondante |
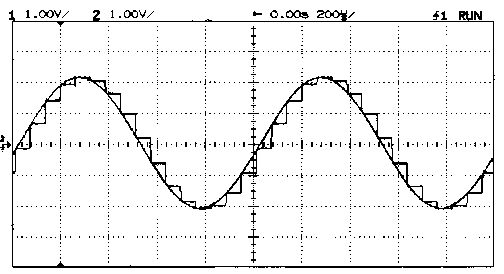 | ||
| Sinusoïde et sinusoïde échantillonnée bloquée | ||
| 200 us / carreau | Voie 1 : 1 V / c | Voie 2 : 1 V / c |
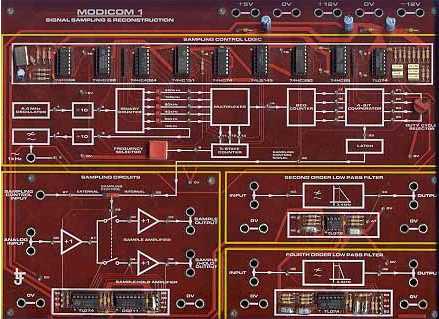 |
| Carte de Travaux Pratiques "Modicom1, de Delta Lab" |
fin de l'article 19