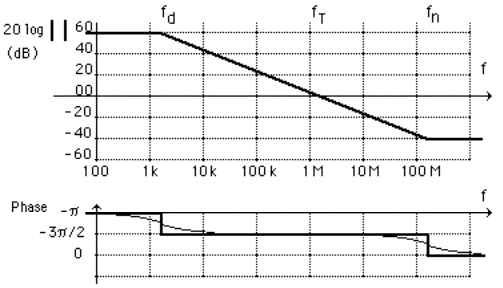
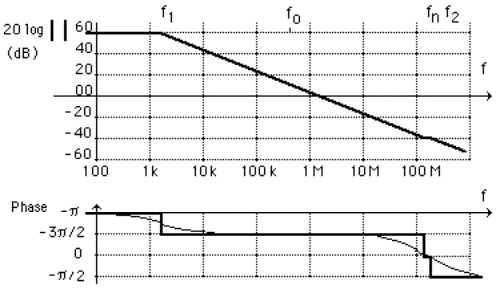
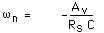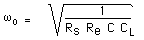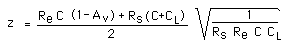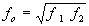Comprendre l'électronique par la simulation.
par Serge Dusausay  Espace lecteur  plan du site


 Article 17 
   Quelques informations supplémentaires des pages 105 à 108 du livre.


L'article 17 montre, au travers de la simulation d'un montage à base d'amplificateur, une réponse exacte et une réponse d'un circuit simplifié par le théorème de Miller.
L'équation exacte est donnée en page 107 du livre, sous référence [8].
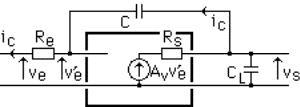
- On se propose ci-dessous de faire l'application numérique du schéma simulé en paragraphe 2.a., afin de la rattacher à la simulation montrée en page 108.
- Une extension au schéma est également proposée et son analyse correspondante : il s'agit de placer une charge capacitive.

Application numérique
Les valeurs des composants donnent :
fn = 159,15 MHz
fd = 1574 Hz.
Un tracé rapide des réponses asymptotiques est présentée ci-dessous :
réponse harmonique idéalisée
Diagrammes asymptotiques de Bode du circuit de la page 107 ;
un tracé qualitatif de la courbe de phase a été ajoutée

Interprétation :

1) On reconnait les fréquences caractéristiques données dans le livre, en page 108 :
. fd = 1,6 kHz environ
. fT = 1,6 MHz environ

2) On vérifie que lorsque f tend vers l'infini, la fonction [8] est équivalente à :
vs/ve= Av wd/wn = Av fd/fn
soit, par simple application numérique, vs/ve= - 9,89 10-3, soit - 40 dB de module.
La réponse harmonique se confond à cette asymptote horizontale pour des fréquences supérieure à fn = 160 MHz environ.

3) Pour une meilleure interprétation, ces courbes sont à superposer à celles données en page 108 (courbe dB(v(4), sur le schéma d'origine).

4) Il est bien évident que ces valeurs numériques de fréquence sont liées aux choix des composants proposés dans cet article 17.
Le montage simulé étant à base de source de tension commandée, et non à base d'amplificateur réel, les réponses obtenues sont donc idéalisées, même jusqu'à des fréquences inaccessibles en composants discrets.




Charge capacitive
Le schéma simulé en 2.a peut représenter un modèle d'amplificateur à base de transistor (bipolaire ou Mos) avec le condensateur (CBC ou CGS) placé entre l'entrée et la sortie.
Les calculs donnés dans l'article ont montré que l'utilisation du théorème de Miller permettaient d'obtenir aisément et avec précision la zone basse fréquence de la réponse harmonique, d'où notamment la détermination de la bande passante.
Néanmoins, il est fréquent que la charge de l'amplificateur soit capacitive.
Les calculs et simulations données dans le livre ne traitent pas ce cas.
Nous nous proposons de prolonger l'article par cet essai supplémentaire.
Le schéma à analyser est donc, avec CL :
schéma d'étude
Schéma d'étude : il a été ajouté CL.
Le calcul est similaire à celui donné en page 106 du livre.
Les relations [5], [6] sont inchangées.
Le condensateur CL est parcouru par un courant vs j CLw.
La relation [7] devient :
vs = Av v'e - Rs (ic + vs j CLw)
Par un développement identique à celui présenté en page 106, on aboutit à :
relation
fonction complexe de transfert

avec :
équation de wn
expression de wn

équation de wo
expression de wo

équation de z
expression de z

Supposons l'application numérique inchangée, avec CL = 1 nF.
Il vient :
wn = 109, soit fn = 159,15 MHz
wo = 3,16 Mrad/s, soit fo = 503,3 kHz
z = 161,4...
Le dénominateur d'ordre 2 est à z > 1. Il peut donc être mis sous la forme :
(f-f1)(f-f2)
Soit 2 fréquences de cassure :
f1 = 1,559 kHz et f2 = 162,493 MHz
On a
Ces renseignements permettent de réaliser un tracé rapide des réponses asymptotiques :
réponse harmonique idéalisée
Diagrammes asymptotiques de Bode du circuit ci-dessus.
Un tracé qualitatif de la courbe de phase a été ajoutée.

Pour une meilleure lisibilité, les fréquences fn et f2, qui sont très voisines, ont été espacées. Le plateau entre fn et f2 est donc très réduit.

L'apport du condensateurCL se traduit par un dénominateur d'ordre 2 ce qui apporte les changements suivants :
- la rotation de phase supplémentaire, quand f tend vers l'infini,
- une asymptote oblique de -20 dB/décade, quanf f tend vers l'infini.

En conclusion, dans la gamme des fréquences basses et moyennes, l'apport de la charge capacitive CL = 1 nF n'a quasiment pas modifié la réponse harmonique. L'effet de cette charge est visible pour des fréquences bien au delà de fT, donc sans conséquence pour le montage.

fin de l'article 17

retour à l'écran d'accueil