Comprendre l'électronique par la simulation.
par Serge Dusausay  Espace lecteur  plan du site


 Article 13 
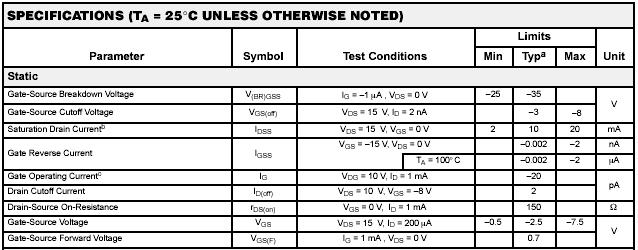
   Quelques informations supplémentaires des pages 85 à 90 du livre.


Dans cette page, on se propose de comparer simulation/pratique du circuit amplificateur à base de 2N3819.
Le montage est câblé conformément au schéma de la page 86 du livre, à l'exception de la résistance série de 100 kOhm qui a été volontairement omise, jusqu'au paragraphe 3.b.


1) Polarisation
Une mesure des différents potentiels donne :
VDS = 8,69 V
VGS = - 0,289 V
ID = 4,24 mA

Les écarts avec la simulation sont justifiés par le fait que le 2N3819 réel est donné avec :
-8V < Vgsoff
2 mA < IDSS < 10 mA
alors que les simulations ont été faites avec les valeurs typiques, c'est à dire :
Vgsoff = - 3 V,
et IDSS = 10 mA

2) Amplification
Un essai dynamique à 1 kHz a été réalisé, avec un signal de faible amplitude, pour rester dans le domaine linéaire.

Est présenté ci dessous :
- le signal d'entrée (Voie 1, 20 mV par carreau),
- le signal de sortie (Voie 2, 200 mV par carreau).
L'axe 0 V est commun aux 2 traces et est au centre de l'écran.

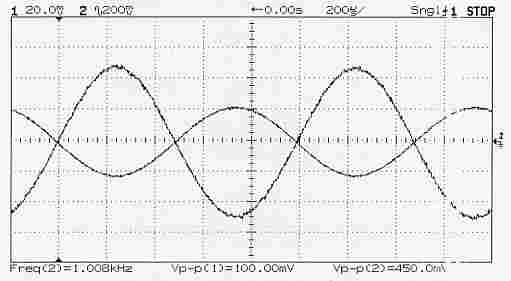
recopie d'écran scannérisée
Fonctionnement de l'amplificateur source commune
200 us / carreau CH1 : 20 m V / c CH2 : 200 mV / c   AC

Interprétation :
- l'amplitude du signal d'entrée est de 50 mV (2,5 carreaux à 20 mV).
- l'amplitude du signal de sortie est environ 225 mV (1,25 carreau à 200 mV).

Le signal de sortie est en opposition de phase.
On déduit une amplification voisine de - 4,5.

Une autre représentation de ces traces permet de vérifier sommairement la linéarité. Il suffit de positionner l'oscilloscope en mode XY.

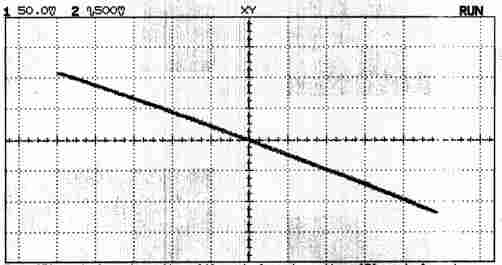recopie d'écran scannérisée
mêmes traces, en XY
CH1 : 50 m V / c CH2 : 500 mV / c   AC

Interprétation :

La trace est une droite, ce qui montre que la sortie suit linéairement l'entrée.
La pente est négative, ce qui rappelle l'aspect inverseur de l'amplificateur.
Une mesure de pente (en tenant compte des calibres) permet de retrouver le coefficient d'amplification de - 4,5.

A titre d'information, voici ce que donne les mêmes essais avec un signal d'entrée de plus forte d'amplitude (ici, les axes sont décalés, pour une meilleure visibilité):
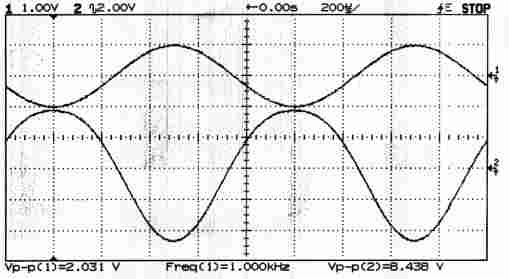recopie d'écran scannérisée
amplificateur en haut niveau : distorsion
200 us / carreau haut : CH1 : 1 V / c bas : CH2 : 2 V / c   AC

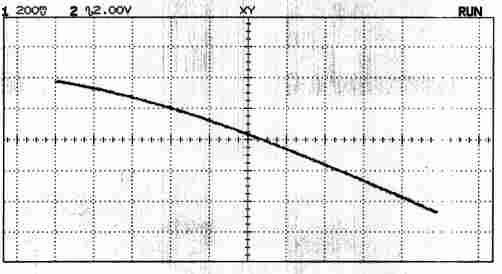recopie d'écran scannérisée
mêmes traces, en XY
CH1 : 200 m V / c CH2 : 2 V / c   AC

Interprétation :
Avec une amplitude d'entrée de 1 V, on perçoit nettement la non linéarité de l'amplificateur source commune, due à l'équation parabolique du transistor JFET.

3) Réponse en fréquence
On travaille en petits signaux (ici, 50 mV d'amplitude à l'entrée).
Rappelons que le signal de sortie est visualisé par un oscilloscope (dont la capacité d'entrée est environ 30 pF) relié par un câble (dont la capacité d'entrée est environ 100 pF). La charge capacitive présente en sortie du montage est donc environ CL = 130 pF.
3.a)
On fait croître la fréquence jusqu'à trouver un signal de sortie qui a perdu 3 dB, soit une multiplication par 0,707. On trouve la fréquence de coupure haute de 1,29 MHz.
Cette valeur est liée à l'environnement de l'amplificateur, (et non au transistor JFET qui "monte" bien plus haut en fréquence).
En effet, le schéma dynamique (page 87) montre Req = 937,5 Ohm.
Il s'ensuit une fréquence de coupure 1/(2 pi Req CL) = 1/(6,28 937,5 130 p) = 1,3 MHz.

Un essai vers les basses fréquences aboutit à 10 Hz.
Ces essais donnent la bande passante de l'étage à JFET sans la résistance additive à l'entrée.

3.b)
Afin de retrouver les résultats de simulation donnés dans le livre, insérons la résistance rg = 100 kOhm.

à savoirIl est important de signaler qu'une mesure directe de VGS est à proscrire :
un dBmètre ou un oscilloscope (dont l'impédance d'entrée est indiquée en article 09, page 66) présenterait une impédance du même ordre de grandeur, ou plus faible, que l'impédance d'entrée du transistor JFET, entre Grille et Source.
Il nous faut donc placer les appareils de mesure en amont de rg, et en sortie de l'amplificateur.

- Avec la résistance rg, en milieu de bande, à 1 kHz, à même signal d'entrée, le signal de sortie est plus faible : on obtient une amplification de -4,1 au lieu de -4,5 précédemment. La raison est évidente : il s'agit du pont diviseur 100 kOhm, 1 MOhm, comme indiqué en page 87.
Il est intéressant de voir que la simulation donnait -4,86 et que la pratique donne -4,1, soit un écart d'envion 20 %, alors que les paramètres IDSS et Vgsoff du transistor sont donnés dans une beaucoup plus grande dynamique.

- Toujours avec la résistance rg, l'essai en fréquence donne une fréquence de coupure haute (à - 3dB) de 62 kHz.
(Dans cette gamme de fréquence, la capacité d'entrée de l'oscilloscope ne perturbe pas cette mesure).
On peut en déduire que la bande passante de tout le montage est réduite par l'étage rg=100 kOhm et les condensateurs de jonction CGS et CGD.
L'écart avec la simulation donnée dans le livre (220 kHz) est lié aux valeurs numériques de ces condensateurs. Or, ces dernières sont tout directement liées à la polarisation, par une loi en exponentielle, ce qui justifie les écarts simulation / pratique des valeurs de bande passante.


4) Pour les plus curieux...

4.a) Détermination de Vgsoff et IDSS du transistor utilisé

Il y a deux inconnues. Il nous faut 2 équations indépendantes.

- On dispose de l'équation parabolique (page 86).
On connait un point de cette parabole : le point de polarisation qu'on notera Io (pour ID) et Vo (pour VGS).

- On dispose de l'expression de gm (page 87), fonction de Io et Vo.

En combinant l'équation parabolique et l'expression de gm, on aboutit à :
Vgsoff = Vo - 2 Io/gm

Faisons l'application numérique.

Polarisation :
Io = 4,24 mA pour le courant drain ; Vo = - 0,289 V pour la tension VGS.
Transconductance :
On connait la valeur de gm, grâce à l'essai en fréquence moyenne, et connaissant les valeurs numériques des composants.
En effet, par Av = gm Req, on déduit gm = 4,5 mA/V.

On calcule alors :
Vgsoff = -2,17 V.
Par suite, en exploitant une des 2 équations, on a : IDSS = 5,64 mA.

Remarque : ces valeurs sont dans les intervalles de valeurs donnés par le constructeur, comme le montre cet extrait de doc ci-dessous :
doc du 2n3819
source Vishay 


4.b) Détermination de CGS et CGD du transistor utilisé

La fréquence de coupure haute fh1 62 kHz est :
fh1 = 1/2 PI rg C.
avec rg = 100 kOhm
On déduit C = 28,5 pF.

Or, C = CGS + (1-Av)CGD, par exploitation du théorème de Miller (page 87)

Pour déterminer CGS et CGD, il nous faut une autre équation.
Le plus simple est de faire un essai supplémentaire, en modifiant la charge RL.
Ce choix permet de conserver la même polarisation, donc les mêmes valeurs aux condensateurs.

Avec RL divisée par 2, on obtient, en mesurant sortie et entrée, Av2 = -3,48.
La fréquence de coupure haute est alors fh2 = 73 kHz.
On en conclut, pour cette configuration C = 24,2 pF.

On dispose donc, en bilan :
28,5 pF = CGS + (1+4,5)CGD
24,2 pF = CGS + (1+3,48)CGD

Système qui donne tout simplement :
CGD = 4,2 pF
CGS = 5,3 pF
et ce à VGS = - 0,289 et VGD = -8,69 V.

Remarque :
Il faut noter que le théorème de Miller est une approximation qui suppose un amplificateur parfait, linéaire. En pratique, le transistor a un comportement en fréquence plus complexe, et il est illusoire d'obtenir une précision du dixième de pF sur les valeurs exactes de CGS et CGD par cette méthode. Néanmoins les ordres de grandeurs sont cohérents.
Une mesure directe (par pont capacimètre qui maintient les tensions de polarisation VGS et VGD) donnerait des valeurs différentes, et plus exacte.

fin de l'article 13

retour à l'écran d'accueil